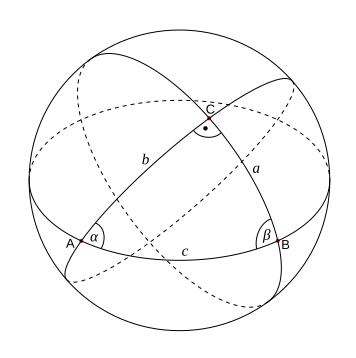
Haversine 公式
Haversine 公式是球面几何中用于计算**球面上两点间最短路径(大圆距离)**的数值稳定公式。源自球面余弦定理,但通过使用半正矢函数避免了小角度下余弦差损失带来的精度问题。
1. 公式目的与应用
目的:
计算球体表面上两点之间的最短弧长距离(大圆距离)。
典型应用:
- 地球表面两点间的真实距离(GPS、地图、LBS)
- 航空航海路线估算
- GIS 地理信息系统
输入:两点经纬度(弧度)、地球半径
输出:大圆距离 d
2. 数学符号定义
| 符号 | 描述 | 单位 |
|---|---|---|
| \varphi_1,\ \varphi_2 | 点 A、B 的纬度 | 弧度 |
| \lambda_1,\ \lambda_2 | 点 A、B 的经度 | 弧度 |
| \Delta\varphi | 纬度差:\ \varphi_2 - \varphi_1 | 弧度 |
| \Delta\lambda | 经度差:\ \lambda_2 - \lambda_1 | 弧度 |
| R | 球体半径(地球约 6371\ \text{km}) | 长度 |
| d | 两点间距离 | 长度 |
3. 数学推导
3.1 半正矢函数
半正矢(Haversine)定义:
\ \operatorname{haversin}(\theta) = \dfrac{1 - \cos\theta}{2} = \sin^2\left(\dfrac{\theta}{2}\right)\ ;
弧长公式:
\ d = R \cdot \theta\ ;
3.2 推导过程
① 球面余弦定理
\ \cos\theta = \sin(\varphi_1)\sin(\varphi_2) + \cos(\varphi_1)\cos(\varphi_2)\cos(\Delta\lambda)\ ;
② 引入半正矢变换
\ \operatorname{haversin}(\theta) = \dfrac{1 - \cos(\theta)}{2} ;
代入余弦定理得到:
\ \operatorname{haversin}(\theta) = \dfrac{1 - [\sin\varphi_1\sin\varphi_2 + \cos\varphi_1\cos\varphi_2\cos(\Delta\lambda)]}{2}\ ;
③ 使用半正矢恒等式
\ \operatorname{haversin}(\theta) = \operatorname{haversin}(\Delta\varphi)\cos(\varphi_1)\cos(\varphi_2)\operatorname{haversin}(\Delta\lambda)\ ;
④ 写成显式形式(常用)
\ \sin^2\left(\frac{\theta}{2}\right) = \sin^2\left(\frac{\Delta\varphi}{2}\right)\cos(\varphi_1)\cos(\varphi_2)\sin^2\left(\frac{\Delta\lambda}{2}\right)\ ;
⑤ 定义中间变量
\ a = \sin^2\left(\frac{\Delta\varphi}{2}\right)\cos(\varphi_1)\cos(\varphi_2)\sin^2\left(\frac{\Delta\lambda}{2}\right)\ ;
⑥ 求圆心角 \theta
主公式:
\ \theta = 2\arcsin(\sqrt{a})\ ;
数值更稳定的版本:
\ \theta = 2\arctan\left(\dfrac{\sqrt{a}}{\sqrt{1-a}}\right)\ ;
4. 最终公式(Haversine 距离公式)
\ \boxed{ d = 2R \cdot \arctan\left(\dfrac{\sqrt{a}}{\sqrt{1-a}}\right) }
其中:
\ a = \sin^2\left(\frac{\Delta\varphi}{2}\right)\cos(\varphi_1)\cos(\varphi_2)\sin^2\left(\frac{\Delta\lambda}{2}\right)
5. 实际计算步骤(工程实现)
- 经纬度从度数转为弧度
- 计算差值:
- \ \Delta\varphi = \varphi_2 - \varphi_1
- \ \Delta\lambda = \lambda_2 - \lambda_1
- 计算中间量 a
- 计算圆心角 \ \theta = 2\arctan\left(\frac{\sqrt{a}}{\sqrt{1-a}}\right)
- 计算距离:\ d = R\theta
6. 公式的优点与局限
优点
- 小角度(近距离)计算非常稳定
- 不会发生余弦差导致的精度丢失
- 适合大多数地理、工程场景
- 实现简单,性能优秀
局限
- 假设地球为完美球体
- 存在约 0.3% 的系统误差
- 不适合厘米级精度场景(航空、大地测量)
- 可使用 Vincenty 公式替代
7. 历史背景
Haversine 来自 “half-versed sine”,是航海与天文学用于查表的函数。
其主要目的就是避免余弦计算带来的负值处理与精度问题。
8. 关键参数与误差
地球半径常用值:
- 平均值:6371\ \text{km}(推荐)
- 赤道半径:6378.137\ \text{km}
- 极半径:6356.752\ \text{km}
误差来源:
- 使用球体模型替代椭球体
- 近极地区效果略差
9. Haversine 与球面余弦定理的比较
| 特性 | Haversine 公式 | 球面余弦定理 |
|---|---|---|
| 数值稳定性 | 高(近距离无精度损失) | 低(小角度误差明显) |
| 计算复杂度 | 稍高 | 较低 |
| 适用场景 | 通用,特别适合短距离计算 | 适合大角度场景 |
10. 总结以及代码实现
Haversine 是计算球面大圆距离最稳定、最实用的数学公式之一。由于地球并非完美球形故使用此算法计算距离较远时误差较大,
为解决一般采用 Vincenty 算法(基于椭球模型计算其表面两点距离的迭代算法)
java实现的Haversine以及 Vincenty 算法
DistanceCalculateUtil.java
package com.bingbaihanji.app.springboot.utils.geo;
import lombok.extern.slf4j.Slf4j;
/**
* 距离计算工具类
* <p>
* 实现 Haversine 与 Vincenty 公式,用于计算地球表面两点之间的最短距离(大地线距离)。
* Vincenty 基于椭球模型,更精确;Haversine 基于球体模型,速度更快。
* <p>
* 作者:bingbaihanji
* 日期:2025-11-25
*/
@Slf4j
public final class DistanceCalculateUtil {
private DistanceCalculateUtil() {
throw new IllegalStateException("禁止实例化");
}
/**
* 地球平均半径(米)
*/
private static final double EARTH_RADIUS = 6371000.0;
/**
* WGS-84 椭球参数
*/
private static final double A = 6378137.0; // 长半轴
private static final double B = 6356752.314245; // 短半轴
private static final double F = 1 / 298.257223563; // 扁率
/**
* Vincenty 迭代最大次数
*/
private static final int VINCENTY_MAX_ITER = 40;
/**
* 使用Haversine公式计算两个经纬度点之间的地球表面距离
*
* @param lat1 第一个点的纬度(十进制度数)
* @param lon1 第一个点的经度(十进制度数)
* @param lat2 第二个点的纬度(十进制度数)
* @param lon2 第二个点的经度(十进制度数)
* @return 两点之间的地球表面距离(单位:米)
*/
public static double calculateHaversineDistance(double lat1, double lon1,
double lat2, double lon2) {
validateLatLon(lat1, lon1);
validateLatLon(lat2, lon2);
// 将角度差转换为弧度
double dLat = Math.toRadians(lat2 - lat1);
double dLon = Math.toRadians(lon2 - lon1);
// 将纬度转换为弧度
double radLat1 = Math.toRadians(lat1);
double radLat2 = Math.toRadians(lat2);
// 计算半正矢公式中的正弦值
double sinDLat = Math.sin(dLat / 2.0);
double sinDLon = Math.sin(dLon / 2.0);
// 应用Haversine公式计算球面距离
double a = sinDLat * sinDLat +
Math.cos(radLat1) * Math.cos(radLat2) *
sinDLon * sinDLon;
// 计算中心角
double c = 2.0 * Math.atan2(Math.sqrt(a), Math.sqrt(1 - a));
// 计算实际距离(弧长乘以地球半径)
double distance = EARTH_RADIUS * c;
log.trace("Haversine距离计算完成:{} m", distance);
return distance;
}
/**
* 使用 Vincenty 公式计算两个经纬度点之间的椭球大地线距离(单位:米)。
* <p>
* 该方法基于 WGS-84 椭球模型,通过迭代求解椭球面上两点间的最短路径(大地线)长度,
* 精度高但可能在某些极端情况下不收敛。
* </p>
*
* @param lat1 第一个点的纬度(十进制度数)
* @param lon1 第一个点的经度(十进制度数)
* @param lat2 第二个点的纬度(十进制度数)
* @param lon2 第二个点的经度(十进制度数)
* @return 返回两点间沿地球表面的椭球大地线距离,单位为米;若算法未收敛则返回 NaN
*/
public static double calculateVincentyDistance(double lat1, double lon1,
double lat2, double lon2) {
validateLatLon(lat1, lon1);
validateLatLon(lat2, lon2);
// 将经度差转换为弧度
double L = Math.toRadians(lon2 - lon1);
// 计算降纬度(辅助球面坐标)
double U1 = Math.atan((1 - F) * Math.tan(Math.toRadians(lat1)));
double U2 = Math.atan((1 - F) * Math.tan(Math.toRadians(lat2)));
double sinU1 = Math.sin(U1), cosU1 = Math.cos(U1);
double sinU2 = Math.sin(U2), cosU2 = Math.cos(U2);
double lambda = L;
double lambdaPrev;
double sinSigma, cosSigma, sigma;
double cosSqAlpha = 0;
double cos2SigmaM = 0;
int iter = VINCENTY_MAX_ITER;
// 迭代计算 lambda 直到收敛或达到最大迭代次数
do {
double sinLambda = Math.sin(lambda);
double cosLambda = Math.cos(lambda);
// 计算 sigma 的正弦值(球面三角中的边长)
sinSigma = Math.sqrt(
(cosU2 * sinLambda) * (cosU2 * sinLambda) +
(cosU1 * sinU2 - sinU1 * cosU2 * cosLambda) *
(cosU1 * sinU2 - sinU1 * cosU2 * cosLambda)
);
// 若两点重合,则直接返回 0 距离
if (sinSigma == 0) return 0;
cosSigma = sinU1 * sinU2 + cosU1 * cosU2 * cosLambda;
sigma = Math.atan2(sinSigma, cosSigma);
// 计算方位角的正弦,并用于后续修正项计算
double sinAlpha = cosU1 * cosU2 * sinLambda / sinSigma;
cosSqAlpha = 1 - sinAlpha * sinAlpha;
// 处理赤道线情况下的特殊值
if (cosSqAlpha == 0) {
cos2SigmaM = 0;
} else {
cos2SigmaM = cosSigma - 2 * sinU1 * sinU2 / cosSqAlpha;
}
// 计算修正系数 C
double C = F / 16 * cosSqAlpha * (4 + F * (4 - 3 * cosSqAlpha));
lambdaPrev = lambda;
// 更新 lambda 值进行下一次迭代
lambda = L + (1 - C) * F * sinAlpha *
(sigma + C * sinSigma * (cos2SigmaM +
C * cosSigma * (-1 + 2 * cos2SigmaM * cos2SigmaM)));
} while (Math.abs(lambda - lambdaPrev) > 1e-12 && --iter > 0);
// 判断是否收敛,如未收敛记录警告并返回 NaN
if (iter == 0) {
log.warn("Vincenty公式未收敛");
return Double.NaN;
}
// 计算椭球修正因子 u^2
double uSq = cosSqAlpha * (A * A - B * B) / (B * B);
// 计算大地线长度修正系数 A 和 B
double bigA = 1 + uSq / 16384.0 *
(4096 + uSq * (-768 + uSq * (320 - 175 * uSq)));
double bigB = uSq / 1024.0 *
(256 + uSq * (-128 + uSq * (74 - 47 * uSq)));
// 最终修正项 deltaSigma
double deltaSigma = bigB * sinSigma *
(cos2SigmaM + bigB / 4.0 *
(cosSigma * (-1 + 2 * cos2SigmaM * cos2SigmaM) -
bigB / 6.0 * cos2SigmaM *
(-3 + 4 * sinSigma * sinSigma) *
(-3 + 4 * cos2SigmaM * cos2SigmaM)));
// 返回最终的距离结果(米)
return B * bigA * (sigma - deltaSigma);
}
/**
* 验证给定的纬度和经度值是否有效。
*
* @param lat 纬度值
* @param lon 经度值
*/
private static void validateLatLon(double lat, double lon) {
if (lat < -90 || lat > 90) {
throw new IllegalArgumentException("纬度必须在 -90 到 90 之间");
}
if (lon < -180 || lon > 180) {
throw new IllegalArgumentException("经度必须在 -180 到 180 之间");
}
}
}